今天的題目原出處是 №1029 (https://leetcode.com/problems/two-city-scheduling/),算是較新的題目。簡單來說就是有 2N 個人要把他們丟到 A 跟 B 兩個城市,每個人要被丟到 A 或 B 都有各自的 Cost,最後關鍵的是兩個城市最後都要有 N 個人囉!
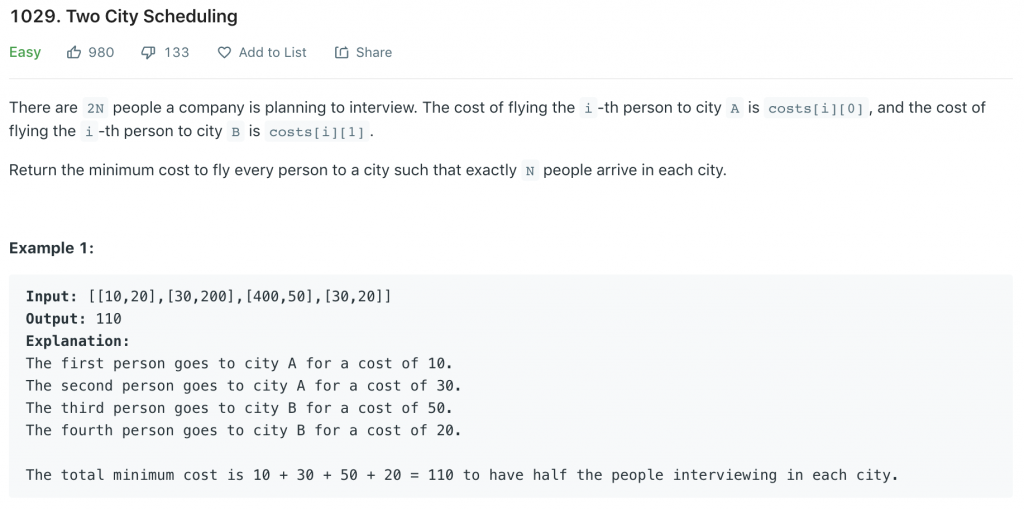
一開始可能會想說,那我就先 “貪婪地” (greedy) 把丟到 A 的 Cost 先排序,把前 N 低的,丟到 A,剩下的人再丟到 B,但很明顯這是有問題的,假設以 Example 1 來說,我們先用丟到 A 的 Cost 進行排序得到 [10, 20], [30, 20], [30, 200], [400, 50] ,結果反而讓丟到 B 的 Cost 大爆炸 (200+50)。反過來根據 B 的 Cost 排序當然也有問題 (你怎麼知道要用 A 還是 B 的 Cost 來排序?!)
所以這題基本上還是可以用 Greedy 的方式,但是要排序 (升序) 的是 “丟到 Cost A 和 Cost B 的差”!我們先以這個思想把 Example 1 排出來會得到 [30, 200], [10, 20], [30, 20], [400, 50] (因為 “差” 的排序是 -170, -10, 10, 350 ),因為這裡只有四個人,所以我們就把前兩個就會丟到 A (30 and 10),後兩個則是丟到 B (20 and 50)。這樣排序的理由是,以 [30, 200] 來說,要是我不選 A (30),而選了 B (200),那麼成本會比選 A 大大地多了 170 ,為了不讓這個情況發生,我這時候更一定要選 A 了,這樣你有感覺了嗎?讓我們再看最後一個 [400, 50] ,要是此時我不選 B,而是選 A,那麼選 A 的成本就會比選 B 的成本大大增加了 350 !相信聰明的人看到這應該已經懂了!那麼最後就讓我們來看 Code 。
Code 的部分就跟上述一模一樣啦!Line 3 作排序,而排序是根據 “丟到 Cost A 和 Cost B 的差” (x[0]-x[1]) ,再來就是把前 N 個的 Cost of A 放到 totalCost,以及把後 N 個的 Cost of B 放到 totalCost 。就醬!
class Solution:
def twoCitySchedCost(self, costs: List[List[int]]) -> int:
sortedCosts = sorted(costs, key=lambda x: x[0] - x[1])
totalCost = 0
for i in range(len(costs)//2):
totalCost += sortedCosts[i][0]
for i in range(len(costs)//2, len(costs)):
totalCost += sortedCosts[i][1]
return totalCost
彩蛋!如果你想要用 DP 的話該怎麼做呢?記得 DP 兩部曲嗎?狀態的定義,以及狀態轉移方程式 (忘記的看 這裡 )。這裡原先的問題是,如果有 2N 個人,其中某 N 個人在 A (代表其他 2N-N=N 的人在 B) 的 Cost,那麼子問題就是如果有 i 個人,其中 j 個人在 A (代表其他 i-j 的人在 B) 的 Cost 是多少。因此 dp[i][j] 就是如果有 i 個人,其中 j 個人在 A 的 Cost 啦!狀態轉移方程式則是 dp[i][j] = min(dp[i-1][j] + costs[i-1][1], dp[i-1][j-1] + costs[i-1][0]) ,就是看 1. 把 i是丟到 A 2. 把i 丟到 B 哪一個成本比較小。(這裡要注意的是 costs[i-1] 的 i-1 是因為這裡 i 是指第 i 個人,但是 costs 是從 0 開始。) 不過 DP 要花的時間跟空間自然比較高囉!(O(N²))
class Solution:
def twoCitySchedCost(self, costs: List[List[int]]) -> int:
dp = [[float('inf') for j in range(len(costs)//2 + 1)] for i in range(len(costs) + 1)]
dp[0][0] = 0
for i in range(1, (len(costs) // 2) + 1):
dp[i][0] = dp[i-1][0] + costs[i-1][1]
for i in range(1, len(costs) + 1):
for j in range(1, len(costs) // 2 + 1):
dp[i][j] = min(dp[i-1][j] + costs[i-1][1], dp[i-1][j-1] + costs[i-1][0])
return dp[len(costs)][len(costs) // 2]
See YA!
歡迎追蹤我的 Medium 囉!
https://medium.com/@ryanyang1221
